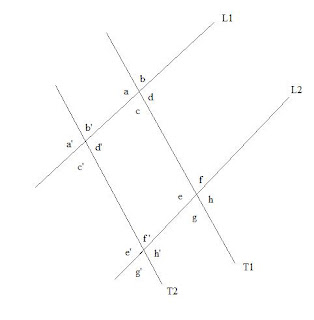
As shown in the diagram lines L1 and L2 are parallel as well as lines T1and T2. Labeling the angles so that angle a and angle a' correspond with each other, we get two lines that shadow each other and allow us to develop all possible relationships between these angles. This simple diagram provides ample practice identifying all the different type of angles and their relative properties, most of which are tested to some degree in most SAT tests.
VERTICAL ANGLES
When a straight line crosses another straight line so that four resulting angles form, two pairs of vertical angles form. For the intersection of line T1 with line L1 the four vertical angles develop a, b, c, d. Thanks to the vertical angles theorem
a=d and b=c
This can be understood if you view the V as being reflected onto itself. In other words angle a is reflected over an imaginary line to form angle d and the same goes for b and c. Can you extend the vertical angles relationship and find all pairs of vertical angles? If so, you should be able to identify 8 pairs of vertical angles.
This is such a simple concept to understand, however, the SAT often requires you to demonstrate practical knowledge by solving problems like these.
Given the following diagram, find the measure of angle x.
Using what we know about vertical angles we can see that angle a = 35* and angle b = 53* since they are diagonally opposite. Since all angles inside of a triangle add up to 180*, we simply note that
a + b + x = 180 Rearranging the equation and solving for x by subtracting a and b from 180 we get
x = 180 - a - b Substituting a = 35* and b = 53* the equation becomes
x = 180 - 35 - 53 Giving us
x = 92*
Another example problem, includes
SUPPLEMENTARY ANGLES
Observe again in the diagram angles along the same line. Take for example e' and g'. First, they result when T2 crosses L2, however, instead of being diagonally opposite each other they are adjacent and along the same line which happens to be T2. The key relationship behind these angles is that they always add to 180 degrees. So, taking the cross section of T1 with L2 we can develop these equations:
e + f = 180
e + g = 180
f + h = 180
g + h = 180
Each intersection of each line in the first diagram produces 4 supplementary angles, and since there are 4 intersections, there are a total of 16 relationships involving supplementary angles.
This example uses what we know about triangles from above and supplementary angles to solve two problems.
Given the following diagram, find the measures of a*, b* and c*.
First spot that angle 32* is along the same line and adjacent to angle c* which allows us to directly apply our knowledge of supplementary angles.
32* + c* = 180* Solving for c* by subtracting 32* from both sides we obtain
c* = 180* - 32* Solving the equation, we get
c* = 148*
Second, we can see that angles 71*, 32* and a are on the interior of a triangle meaning that they add to 180*. Writing out our equation, we describe the relationship as follows:
71* + 32* + a *= 180* Solving for a* by subtracting 71* and 32* from both sides we obtain
a* = 180* - 71* - 32* Solving the equation, we get
a* = 77* (equation 1)
Finally, we spot that b* is along the same line and adjacent to a* and apply what we know about supplementary angles to develop the following relationship:
a* + b* = 180* Solving for b* by subtracting a* we obtain
b* = 180 - a* Substituting a* = 77 from equation 1 above we obtain
b* = 180* - 77* Solving the equation, we get
b* = 103*
CORRESPONDING ANGLES
Looking back at Diagram 1, we can imagine taking angle b and sliding it along line T1 until it occupies the same spot as f and because L1 and L2 are parallel, angles b and f will be the same. Now, applying that to the intersection of L1 with T1, if we were to slide that intersection along T1 until it arrived at the intersection of T1 and L2, we would discover these important relationships:
b = f
a = e
c = g
d = h
At this point, the reason for Diagram 1 exhibiting 2 pairs of parallel lines becomes important, because any intersection can move along a line and produce an amazing number of equal angles. For instance, you can slide the intersection of L1 and T1 along L1 until the intersection sits on top of the intersection of L1 and T2. Then that intersection can glide along the line T2 until it sits on the same intersection of T2 and L2. That same intersection can glide along L2 until we are back at the intersection of L2 and T1. The diagram below shows details of the movements:
So, with using your imagination and picturing the lines gliding along each other you can see how the first intersection moves left, then down, then right then back up to its original location giving the overall relationships:
a = a' = e' = e
b = b' = f ' = f
c = c' = g' = g
d = d' = h' = h
The important thing to remember when gliding intersections along parallel lines is that only the exact replicas remain intact, other transversals can confuse even experienced mathematicians. This next example features such a case and combines what we know about vertical angles, supplementary angles and corresponding angles into a good little skill builder.
Given the that L2 and L1 are parallel lines find angles a, b, c, x, y, and z (figure not drawn to scale).
First thing about this problem, is there are multiple questions and solving one helps you to solve the other. However, on an actual SAT, you are more likely to be given the two angles and asked to solve for a. Which goes to show you, that an involved problem like this often requires multiple steps and different uses of the knowledge we have learned. As such, one possible approach to solving this problem that demonstrates the importance of understanding corresponding angles is as follows:
Notice z* and 25* are vertical angles therefore
z = 25* (equation 1)
Angles z and b are adjacent and along the same line T2 and are therefore supplementary angles giving us the following relationship
b* + z* = 180* solving for b by subtracting z from both sides
b* = 180* - z* substituting using equation 1 we get
b* = 180* - 25* solving we obtain
b* = 155* (equation 2)
At this point we can take a couple approaches to solving for x and y, however, we are going to use our knowledge of corresponding angles to solve for x, and then use what we know about corresponding angles and vertical angles to solve for y. Let's take a look:
Notice the intersection of T2 with L1, and glide it along T2 until it reaches the intersection T2 and L2. Do you see how angle b* = x* + 35*? The transversal T1 splits the corresponding angle of b into two segments. However, because all lines through the intersection are straight, we are still able to apply our corresponding angles relationships. Doing so gives us:
x* + 35 = b* Solving for x* we get
x* = b* - 35* Substituting equation 2 back into the formula we get
x* = 155* - 35* Solving we get
x* = 120* (equation 3)
Now, notice that c and 25* are corresponding angles, therefore:
c* = 25* (equation 4)
Now notice that angle c and angle y are vertical angles, giving us this relationship
y* = c* Substituting with equation 4 we get
y* = 25* (equation 5)
Now lets apply what we know to find the missing angle in the triangle. Notice that whatever that angle might be, it happens to be equal to a by way of being vertical angles. Since all angles in a triangle add to 180* we can simply use what we know from earlier to find a.
x* + z* + a* = 180* Solving for a* by subtracting z* and x* from both sides we get
a* = 180* - x* - z* Substituting with equation 3 and equation 1 for x and z we get
a* = 180* - 120* - 25* Solving we get
a* = 35*
That concludes this lesson, my next post will be on Alternating angles, Interior angles and Complementary angles.